A-Fire on Field
题意:设A[0]=1,A[1]=1,后面的每一项都为不会和前面数字形成下标权值都等差的最小数字。问A[n]。n小于1000
解:暴力。题目给出了一张图,1000以内的答案甚至不会超过300。但是这题我却WA在了没看懂英文:arithmetic progression意为等差数列,我却把其中的progression感受成了有向前、进击、提升意味的词。把它当成了递增等差数列。学好英语,特别要学好专业英语。
I-Thread Knots
LYF 好像是简单二分查找
J-Triangulation
LYF
题意:将正n边形分割成任意个三角形,设其中一个三角形与另一个三角形的距离为最少要走过的三角形个数。问最短的最大距离。
解:考虑各种特殊情况,可以得到猜想:设一次操作为将多边形一半的角作为三角形的一个角
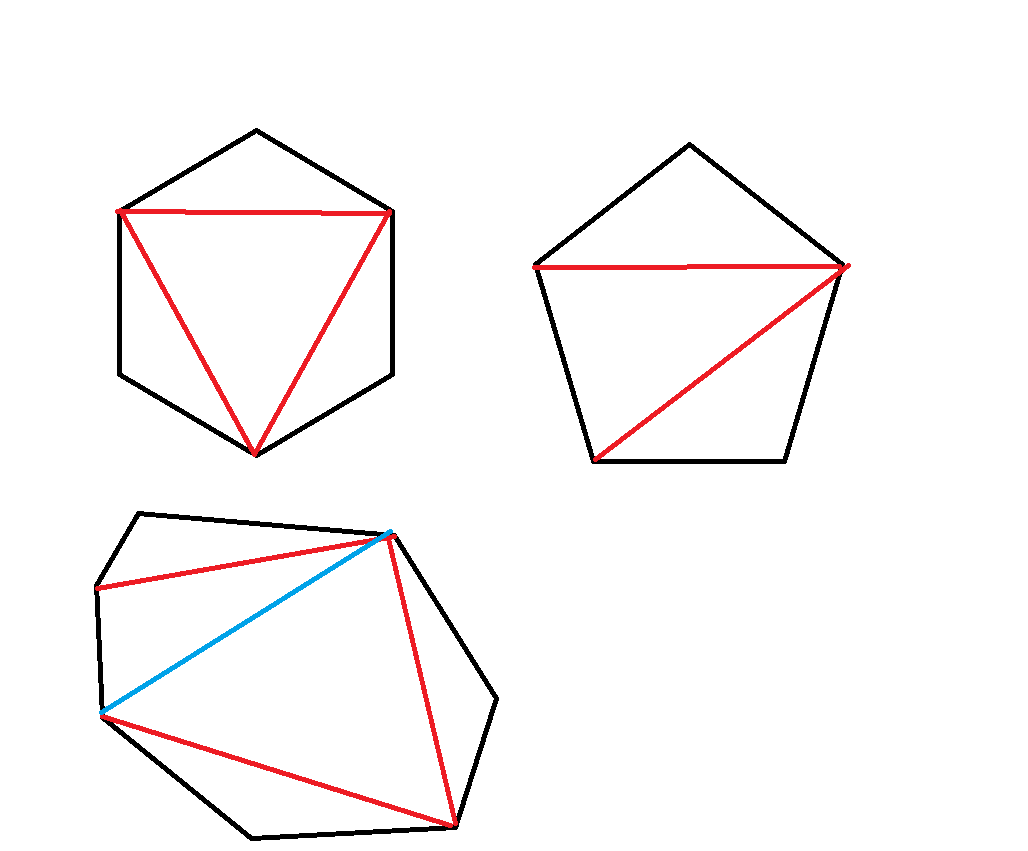
然后对中间剩下的多边形也一直这么操作直到变成两个三角形
感受一下好像是对的举不出反例,交一发就过了
L-What’s Mine is Mine
题意:给定一堆数轴上的线段,它们的权值也给定,问不重复地选择它们得到的最大代价。n小于10000
解:先离散化。然后dp。设f[i]表示已经选的线段的限制不超过i得到的最大代价。因为显然只要限制不超过i,对于之后的决策来讲就是一模一样的。先把线段按照右端点排序。f[i]=max(f[1~i-1],f[left[j]]+w[j])其中right[j]=i。复杂度O(n)
B-Gene Tree
树神WD
K-Washer
WD&少量协作
题意:100个三维点,把所有点分割进两个集合,问两个集合的{集合内三个维度的方差*集合大小}的最小值。
解:枚举其中三个点形成的平面,利用这个平面来分割,暴力计算。复杂度O(n^4)。但是其实枚举时候常数比较小,所以虽然计算过程常数不小但能过。
C-Islands
WD/LYF
题意:两个环上均匀分布$n\le100000$个点,标号从1-n,但是两个环上的顺序不同。问是否存在一个排列使得在两个环上都能按排列的顺序每一步走直线走出一条不会穿过自己的路。
解:首先容易发现如果确定了一个初始点,接下来的每一步目的地都为已走点集的左右两端的未走点,判断两个环上当前步是否有相同的目的地点即可。这是暴力做法。
可以加一个剪枝:观察发现,若在某一个初始点走失败了,则失败前走到的所有点都不可能被当作起始点。感受一下可以发现这玩意基本卡不掉。
补题 H-Strike Zone
题意:二维平面,有红点和蓝点,其中蓝点价值为+c1,红点为-c2,都最多1000个。问平面上所有边和坐标系平行的矩形中包含点价值最大的矩形的价值。保证没有两两相同的x,没有两两相同的y。
解:比赛时候陷入求2000矩阵中最大子矩阵的误区了。看了题解之后回来想又陷入以为正解是$O(n\lg n)$的误区(因为没看数据范围QAQ)。其实显然是扫描线。对于每个点枚举上边界,推下边界,每推一下就加一个点,线段树求和即可,显然。比赛时在矩阵里想过类似做法但是那样就要每一行都扫一遍加点,那肯定是行不通的!要注意到题目的特殊条件限制!!!