DP

前置知识

接下来的题目中用到的默认读者已经掌握的知识：深度优先搜索、二分查找、一些基础的STL函数

如果不知道的话在用到的时候可以自己想办法学一下

介绍

DP，Dynamic Programming，指的是解决问题的一类思路。下面的思考过程直接看是很难看懂的，建议在阅读后面解题思路时回过头来套这样一种思考模式。

思考过程

  1. 将原问题分解为子问题
    把原问题分解为若干个子问题，子问题和原问题形式相同或类似，只不过规模变小了。如果子问题都解决了，原问题就解决了
    子问题的解一旦求出就会被保存，所以每个子问题只需求解一次。
  2. 确定状态
    在用动态规划解题时，我们往往将和子问题相关的各个变量的一组取值，称之为一个“状态”。一个“状态”对应于一个或多个子问题，所谓某个“状态”下的“值”，就是这个“状态”所对应的子问题的解。
  3. 确定一些初始状态（边界状态）的值
  4. 确定状态转移方程
    定义出什么是“状态”，以及在该 “状态”下的“值”后，就要找出不同的状态之间如何迁移――即如何从一个或多个“值”已知的“状态”，求出另一个“状态”的“值” 。状态的迁移可以用递推公式表示，此递推公式也可被称作“状态转移方程”。

具体应用例子可以看“数字三角形”一题

能用DP解决的问题的特点

  1. 问题具有最优子结构性质。如果问题的最优解所包含的子问题的解也是最优的，我们就称该问题具有最优子结构性质。
  2. 无后效性。当前的若干个状态值一旦确定，则此后过程的演变就只和这若干个状态的值有关，和之前是采取哪种手段或经过哪条路径演变到当前的这若干个状态，没有关系。

Naive

数字三角形

思路

首先从朴素想法入手：搜索。以每个最下面一排的位置为起点，向上搜索所有路径。这样的做法的时间复杂度是$O(n\cdot 2^n)$，难以通过本题。或者以最上面的位置为起点，向下搜索所有路径，搜索量是差不多的，思路也差不多，正确性也都可以保证。下面我们以自下而上的情况为例思考。

考虑搜索过程中是否有重复计算的内容。可以发现，对于两条自下而上搜索到一半的路径，如果它们当前的终点是相同的，那么接下来的决策将会相同。也就是说，我们其实可以将“从某个位置出发到最上面的最大路径和”看作一个子问题，显然对于每一个位置都存在这样的子问题，而每个子问题的答案可以只算一遍，算完将其保存下来以备之后查询。因此时间复杂度优化到了$O(n^2)$。这种方法被称为记忆化搜索。（《算法导论》中称为top-down with memoization）

参考代码（记忆化搜索）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include <iostream>
#include <cstring>
using namespace std;
int n,ans,a[111][111],f[111][111];
int dfs(int x,int y)
{
    if (x<=0||y<=0) return 0;
    if (f[x][y]!=-1) return f[x][y];
    return f[x][y]=a[x][y]+max(dfs(x-1,y),dfs(x-1,y-1));
}
int main()
{
    memset(f,-1,sizeof(f));
    cin>>n;
    for (int i=1;i<=n;i++)
        for(int j=1;j<=i;j++) cin>>a[i][j];
    for (int i=1;i<=n;i++) ans=max(ans,dfs(n,i));
    cout<<ans<<endl;
    return 0;
}

反过来思考，从上往下递推，可以发现，如果在求A位置的最大路径和，而又已知左上B和右上C位置的最大路径和，那么在B和C中取更大的，加上A位置的local值，显然即为A位置的最大路径和。由此，可以从上到下按顺序将每个位置的答案求出，时间复杂度$O(n^2)$。这种递推的方法被称为动态规划。（《算法导论》中称为bottom-up method）

根据“介绍”中给的methodology，我们可以这样看这道题目：

  1. 把求解过程分解为若干个子问题，即到各个位置的最大路径和问题
  2. 确定状态：定义$f[i][j]$的含义为从第一行第一列到第$i$行$j$列位置的最大路径和
  3. 确定初始状态：$f[1][1]=a[1][1]$
  4. 状态转移方程：$f[i][j]=a[i][j]+max{f[i-1][j],f[i-1][j-1]}$

显然这道题具有最优子结构性质，也即依靠子问题的最优答案可以直接获得总体的最优答案

显然这道题具有无后效性，后续选择不会影响之前选择的最优性质

样例数据的递推结果（也即记忆化搜索存下来的答案）

7
10 15
18 16 15
20 25 20 19
24 30 27 26 24

对于许多题目，记忆化搜索与递推动态规划都可以作为题目的正确解法，区别仅在于代码实现的复杂度以及搜索所带来的爆栈问题。

大部分DP题都可以模型化成类似的形式，在做后面题目的时候注意应用这样的分析方法，和这道题做比较哦！

参考代码（DP递推）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#include <iostream>
using namespace std;
int n,ans,a[111][111],f[111][111];
int main()
{
    cin>>n;
    for (int i=1;i<=n;i++)
        for(int j=1;j<=i;j++) cin>>a[i][j];
    for (int i=1;i<=n;i++)
        for (int j=1;j<=i;j++)
            f[i][j]=a[i][j]+max(f[i-1][j],f[i-1][j-1]);
    for (int i=1;i<=n;i++) ans=max(res,f[n][i]);
    cout<<ans<<endl;
    return 0;
}

Easy

01背包

思路

如何设计状态？这道题不像数字三角形一样，即使没学过DP也很简单地能设计出状态和转移方程。

可以首先观察这道题中可能可以作为状态的变量：当前已用的时间、可选的草药范围、已取的草药价值

所以我们尝试这样设计：

状态：设$f[i][j]$表示只考虑前$i$种草药的情况下，用$j$时间time（其中部分时间可能是空闲的）所能采到的最大草药价值value

转移方程：$f[i][j]=max{f[i-1][j-t[i]]+v[i],f[i-1][j]}$，max函数中的两项分别代表了取$i$的情况和不取$i$的情况

初态$f[x][0]=0$不管在哪些草药中选择，不花时间肯定采不到草药。

最终答案显然为$f[M][T]$

时间复杂度$O(MT)$，即可解决问题

参考代码（最直观的设计）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include <iostream>
using namespace std;
int M,T,v[11111],t[11111],f[11111][11111];
int main()
{
    cin>>T>>M;
    for (int i=1;i<=M;i++) cin>>t[i]>>v[i];
    for (int i=1;i<=M;i++) 
        for (int j=0;j<=T;j++)
        {
            f[i][j]=f[i-1][j];
            if (j-t[i]>=0) f[i][j]=max(f[i][j],f[i-1][j-t[i]]+v[i]);
        }
    cout<<f[M][T]<<endl;
    return 0;
}

但是，毕竟有三个可以作为状态的量。如果我们换一种设计呢？

状态：$f[i][j]$表示前$i$种草药中选择价值为$j$的草药，所花的最短时间

转移方程$f[i][j]=min{f[i-1][j-v[i]]+t[i],f[i-1][j]}$

初始状态：$f[x][0]=0$，其余为正无穷（将数组预处理为一个不会影响答案的大数即可）

最终答案即为$f[i][j]<T$可能取到的最大的$j$

时间复杂度$O(M\sum v_i)$

这里其实用到了一些贪心的想法。如何证明这样的算法是正确的？

参考代码（另外一种解法）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include <iostream>
#include <cstring>
using namespace std;
int M,T,v[11111],t[11111],f[11111][11111],ans;
int main()
{
    cin>>T>>M;
    for (int i=1;i<=M;i++) cin>>t[i]>>v[i];
    memset(f,0x3f,sizeof(f));//memset是逐字节填充，因此填0x3f就能把f变成都是0x3f3f3f3f的数组
    for (int i=0;i<=M;i++) f[i][0]=0;
    for (int i=1;i<=M;i++) 
        for (int j=1;j<=10000;j++)
        {
            f[i][j]=f[i-1][j];
            if (j-v[i]>=0) f[i][j]=min(f[i][j],f[i-1][j-v[i]]+t[i]);
            if (f[i][j]<=T) ans=max(ans,j);
        }
    cout<<ans<<endl;
    return 0;
}

但是如果这道题的数据范围有变化，比如$T$很大的话就不能用第一种设计，总价值很大的话就不能用第二种设计。因此，在设计好状态之后，不仅应该判断这样的设计在代码实现上可不可行、正确性能否保证，还必须分析复杂度，并根据题目的数据范围分析可不可行。

滚动数组优化

空间复杂度的限制虽然在很多算法题中没有体现，但也是一般编程中必须考虑的问题。以第一种解法为例，我们可以发现，在$i$不断增大的过程中，我们只需要用到$f[i-1]$中的信息，而不需要$f[1\sim i-2]$中的任何数据。所以我们可以尝试把$f$数组改成两行的数组f[2][11111]：

1
2
3
4
5
6
7
8
9
10
11
12
int now=0;
for (int i=1;i<=M;i++) 
{
    now^=1;
    //for (int j=T;j>=0;j--) 如果for循环这样写，改变j的枚举顺序，显然不会影响答案的正确性。但这样的修改可以让我们有下面的进一步优化
    for (int j=0;j<=T;j++)
    {
        f[now][j]=f[now^1][j];
        if (j-t[i]>=0) f[now][j]=max(f[now][j],f[now^1][j-t[i]]+v[i]);
    }
}
cout<<f[now][T]<<endl;

我们知道，在计算机运行程序的时候，一维数组的寻址就是一次size_t的加法，而二维数组的寻址却是一次乘法和一次加法，因此二维数组寻址会慢得多。上面这种方法中编译器很可能会将两行的二维数组寻址优化为一维数组寻址，但是我们也不确定编译器的行为。那能否将代码优化成真正的一维数组呢？这道题中当然是可以的，但是需要注意$j$的枚举方向，不能把需要的数据覆盖了。在上面的方法中，要计算$f[now][j]$的值，只需要知道$f[other][<j]$的值，因此我们可以改变枚举顺序，用$j$从大到小的顺序计算$f[now][j]$，使得不再需要区分$now$和$other$。

1
2
3
4
for (int i=1;i<=M;i++) 
    for (int j=T;j>=0;j--)
        if (j-t[i]>=0) f[j]=max(f[j],f[j-t[i]]+v[i]);
cout<<f[T]<<endl;

一下子想不清楚的话可以带入一组样例并手推或者把每一步的结果打印出来看看。

在时间和空间都不断优化的过程中，我们的代码也越来越短，真奇妙！

上面的另一种设计方法也可以利用滚动数组优化，可以自己试试。

最长公共子序列

思路

子序列即在原序列中选择一部分元素。

两个可以用作状态设计的值为：从第一个序列中的前$i$个中选择，从第二个序列中的前$j$个中选择。

状态转移方程很容易列出

更具体的解题过程与证明可以看《算法导论》

参考代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include <cstring>
#include <iostream>
using namespace std;
const int maxn=5555;
char s[maxn],t[maxn];
int f[maxn][maxn];
int main()
{
    cin>>(s+1)>>(t+1);//为了避免访问到负数位置
    int l1=strlen(s+1),l2=strlen(t+1);
    for (int i=1;i<l1;i++)
        for (int j=1;j<l2;j++)
        {
            f[i][j]=max(f[i][j-1],f[i-1][j]);
            if (s[i]==t[j]) f[i][j]=max(f[i][j],f[i-1][j-1]+1);
        }
    cout<<f[l1-1][l2-1]<<endl;
    return 0;
}

Medium

最长上升子序列

思路

有了前几题的经验，我们可以先列一下什么变量可能可以拿来设计状态：

从序列的前$i$个元素中选择、上升子序列的长度、上升子序列末尾位的大小

很直观地想到这两种状态设计：

设计一

定义$f[i][j]$为从序列前$i$个中取，末尾值为$j$时的最长上升子序列长度

转移方程：$f[i][j]=\max {f[i-1][<j]}+1$

但是$j$的取值范围是$10^9$，看似无法解决这道题。实际上，这里可以应用一种被称作“离散化”的方法：由于原数组最多只有$10^6$种取值，且只要数组元素之间的大小关系不变，最终答案就是不变的，因此我们可以从小到大给原数组重新赋值（或者说是映射）成1，2，3，…，n。而这个过程可以利用STL中的map/unordered_map或是自己实现平衡树或哈希表解决。

1
2
3
4
5
6
7
//将a数组离散化
map<int,int> m;
for (int i=1;i<=n;i++) b[i]=a[i];
sort(b+1,b+n+1);
int nn=unique(b+1,b+n+1)-b-1;
for (int i=1;i<=nn;i++) m[b[i]]=i;
for (int i=1;i<=n;i++) a[i]=m[a[i]];

那么，将$j$的取值范围从$10^9$优化到$10^6$之后，显然我们的问题还没有解决。先尝试写一下核心部分的代码：

1
for (int i=1;i<=n;i++)    for (int j=1;j<=n;j++)    {        int temp=0;        for (int k=1;k<j;k++) temp=max(temp,f[i-1][k]);        f[i][j]=temp+1;    }

看似需要$O(n^3)$的时间复杂度才能解决。

但这里我们可以使用一种非常简单高效的优化：

1
for (int i=1;i<=n;i++)    for (int j=1;j<=n;j++)    {        f[i][j]=m[i-1][j-1]+1;        m[i][j]=max(f[i][j],m[i][j-1]);    }

通过设计一个数组m存储f的前缀max值（$m[i][j]=\max{f[i][k]},k\in [1,j]$），将复杂度优化至$O(n^2)$。但$n$的范围$10^6$仍然让我们望而却步。

设计二

定义$f[i][j]$为从序列前$i$个中取，规定上升子序列长度为$j$时的最小末尾值（无穷大表示不存在这样的子序列）

转移方程：
$$
\begin{cases}
f[i][j]=\min {f[i-1][j],a[i]},~~~f[i-1][j-1]<a[i]且i\not=j
\
f[i][j]=f[i-1][j],~~~~~~~~~~~~~~~~~~~~~f[i-1][j-1]\ge a[i]且i\not=j\
f[i][j]=a[i],~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~f[i-1][j-1]<a[i]且i=j\
f[i][j]=\infin,~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~f[i-1][j-1]\ge a[i]且i=j
\end{cases}
$$
这样我们就又得到了一种$O(n^2)$的算法。

参考代码
1
#include <bits/stdc++.h>using namespace std;const int maxn=5555;int n,f[maxn][maxn],a[maxn];int main(){	cin>>n;	for (int i=1;i<=n;i++) cin>>a[i];	f[0][0]=0x3f3f3f3f;	int ans=0;	for (int i=1;i<=n;i++)	{		for (int j=1;j<=i;j++)		{			if (i==j) 			{				if (f[i-1][j-1]<a[i]||j==1) f[i][j]=a[i];				else f[i][j]=0x3f3f3f3f;			}			else if (f[i-1][j-1]<a[i]) f[i][j]=min(f[i-1][j],a[i]);			else f[i][j]=f[i-1][j];			//cout<<f[i][j]<<' ';			if (f[i][j]!=0x3f3f3f3f) ans=max(ans,j);		}		//cout<<endl;	}	cout<<ans<<endl;	return 0;}

突破口在哪里？寻找$f$数组可以利用的性质。可以发现，当$f[i][j]$中$j$增大时，最小末尾值必定增大，也就是说$f[i]$是单调递增的。而且$f[i]$与$f[i-1]$只有一个位置不同，即$f[i-1][j-1]$与$a[i]$大小关系的临界点处。（可以写个程序跑一跑输出一下试试，并想一想为什么）

这样的有序数列找位置问题可以利用二分查找解决。

由此，我们找到了一个优化：定义$f[x]$表示长度为$x$的上升子序列的最小末尾值(为了防止与上面说的$i$相混淆，这里用了$x$)

状态转移方程比较难表示，但代码很简短。具体参看代码。

参考代码
1
#include <cstdio>#include <algorithm>#include <cstring>#include <map>using namespace std;const int maxn=1111111;int n,a[maxn],f[maxn];int main(){	scanf("%d",&n);	for (int i=1;i<=n;i++) scanf("%d",a+i);	memset(f,0x3f,sizeof(f));//将f的所有项赋值为无穷大	f[0]=0;	int ans=0;	for (int i=1;i<=n;i++)	{		int pos=upper_bound(f,f+n+1,a[i]-1)-f;		ans=max(ans,pos);		f[pos]=min(f[pos],a[i]);	}	printf("%d\n",ans);	return 0;}

从这道题我们又得到了启发：不同的状态设计可能某些可以优化，某些却难以更进一步。当你在一种设计中绕啊绕的时候，不妨想一想别的设计方法。

卡牌游戏

思路

应该怎么设计状态？我们很直观地可以得到一些设计的方法：

比如$f[i][j]$表示左边已经被取了$i$个，右边被取了$j$个时的先手最大值。但是这样设计出来的并不是动态规划所需要的“子问题”。即使求出了$f$的所有项，也无法得到所需的最终答案。

对于这种问题，我们有一个比较常用的思路：定义$f[i][j]$为只考虑从第$i$个到第$j$个这一段的双方最优情况下先手取到的值，那么最终答案显然是$f[1][n]$。（注意：这里所说的先手指的是只考虑这一段的局部先手，即假设整个游戏只有这一段时拿第一个的人，而不是特指题目条件中的那个先手玩家）

但是状态转移方程是什么呢？由于这道题有先手方和后手方，他们会有不一样的决策，很难直接想出转移的式子。于是我们考虑$f[i][j]$所依赖的是哪些子问题。在$f[i][j]$中，先手需要选择取$a[i]$还是取$a[j]$。取完之后，先手玩家将会变成后手玩家，段长也小了1（从$i$到$j-1$或者从$i+1$到$j$）。所以我们需要知道这两种情况下后手玩家（与$f[i][j]$情况下的先手是同一个人）所拿到的值，就能分析出$f[i][j]$情况下先手应该拿第$i$个还是第$j$个。

那么我们考虑再引入$g[i][j]$，表示从$i$到$j$这段的双方最优决策下，后手所取到的值。

那么转移方程就比较显然了：

$f[i][j]$的状态有拿走左边或者拿走右边两种选择，而先手方一定选择结果更大的一种情况。拿完这一步之后，先手方就会变成下一步情况下的后手方，接下来能拿到的最大值即$g[i+1][j]$或$g[i][j-1]$的值。

而对于$g[i][j]$来说，此时先手想要自己最大也即对方最小（因为总和是一定的），就是希望自己拿完这一步后到达的$f[i+1][j]$或$f[i][j-1]$最小。
$$
f[i][j]=\max{g[i+1][j]+a[i],g[i][j-1]+a[j]}\
g[i][j]=\min{f[i+1][j],f[i][j-1]}
$$
注意一下$i$和$j$的枚举顺序即可。可以像下面参考代码一样的顺序，也可以把$j-i$（即段长）作为枚举变量，由短至长进行枚举。想清楚枚举顺序想必并不是那么难。

参考代码
1
#include <iostream>using namespace std;const int maxn=3333;int n,a[maxn];long long f[maxn][maxn],g[maxn][maxn];int main(){	cin>>n;	for (int i=1;i<=n;i++) 	{		cin>>a[i];		f[i][i]=a[i];	}	for (int j=1;j<=n;j++)		for (int i=j-1;i>=1;i--)		{			g[i][j]=min(f[i+1][j],f[i][j-1]);			f[i][j]=max(g[i+1][j]+a[i],g[i][j-1]+a[j]);		}	cout<<f[1][n]<<endl;	return 0;}

这道题我们在状态设计中尝试引入了$f$和$g$两个以便于分析，这是很多偏难的问题中必备的方法。

[NOI1995] 石子合并

思路

状态：定义$f[i][j]$为从$i$到$j$这段合并的花费

转移方程：$f[i][j]=\min{f[i][k]+f[k+1][j]+sum(i,j)},k\in [i,j-1]$

注意$i,j$的枚举顺序即可，和上一题类似，只要别让先算的项要依赖后算的项才能算出正确答案就行。

这样我们就得到了一个$O(n^3)$的算法，80分。但是本题需要$O(n^2)$以下才能拿到更多分数，涉及到高深的四边形不等式优化，有兴趣的读者可以在网络上学习。

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include <iostream>
#include <cstring>
using namespace std;
const int maxn=4444;
int n,a[maxn],s[maxn];
long long f[maxn][maxn];
int sum(int l,int r){return s[r]-s[l-1];}
int main()
{
    cin>>n;
    for (int i=1;i<=n;i++) cin>>a[i];
    for (int i=1;i<=n;i++) s[i]=s[i-1]+a[i];
    memset(f,0x3f,sizeof(f));
    for (int i=1;i<=n;i++) f[i][i]=0;
    for (int i=n;i>=1;i--) 
        for (int j=i+1;j<=n;j++) 
            for (int k=i;k<j;k++) 
                f[i][j]=min(f[i][j],f[i][k]+f[k+1][j]+sum(i,j));
    cout<<f[1][n]<<endl;
    return 0;
}

整齐打印

和上一题有一点相似但也不是很相似。这里只贴一份参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include <iostream>
#include <cstring>
using namespace std;
const int maxn=10001;
int n,m,l[maxn],s[maxn];
long long f[maxn];
inline long long cube(int x){return (long long)x*x*x;}
inline long long w(int l,int r){return cube(m-r+l-(s[r]-s[l-1]));}//如果把l到r这段放在同一行，将会产生多少花费
int main()
{
    cin>>n>>m;
    for (int i=1;i<=n;i++) cin>>l[i];
    for (int i=1;i<=n;i++) s[i]=s[i-1]+l[i];
    memset(f,0x3f,sizeof(f));
    f[0]=0;
    for (int i=1;i<=n;i++)
        for (int j=i;j>=1;j--)
        {
            long long temp=w(j,i);
            if (temp>=0) f[i]=min(f[i],temp+f[j-1]);//如果最后一行也要算花费，那么前i个单词隔成任意行后的总花费最小是多少
            else break;
        }
    long long ans=f[n];
    for (int i=n;i>=1;i--) 
    {
        if (w(i,n)>=0) ans=min(ans,f[i-1]);//从第i个单词开始到最后一个单词都放在最后一行的话，总答案将会是多少（因为最后一行的空格不算进答案）
        else break;
    }
    cout<<ans<<endl;
    return 0;
}

Hard

双调巡游

思路

网上有很多本题的解析，思路比较常规。

这里提供一种不一样的思考

类似方法的一篇博客https://www.jxtxzzw.com/archives/3493他讲得篇幅较大，也比较清楚

下面代码的思路：首先将双调巡游过程看成两个人A和B从排好序后的1号点走到n号点，他们路上经过的点均不重复。那么这两个人是相互等价的，交换身份后答案仍然相同。而这个过程中相当于各个点只是需要被分配给A走或分配给B走。（在下面，我默认某个点分配了就是人走到了）

定义$f[i][j]$表示走得慢的人走到了$i$处，且前$i$个点都已经被分配（模拟两个人向右走的过程，那么如果前$i$个点没被分配完，他们也不能回头去走了）、快的人已经走到第$j$个的位置（但不经过$i$到$j$之间的任何点）时的最小花费。

囿于笔者文字水平限制，读者请尽量意会一下。

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include <iostream>
#include <cmath>
using namespace std;
const int maxn=10001;
int n;
pair<float,float> p[maxn];
float f[maxn][maxn];
float sqr(const float &x){return x*x;}
float dis(const pair<float,float> &a,const pair<float,float> &b)
{
    return sqrt(sqr(a.first-b.first)+sqr(a.second-b.second));
}
int main()
{
    cin>>n;
    for (int i=1;i<=n;i++) cin>>p[i].first>>p[i].second;
    sort(p+1,p+n+1);
    for (int i=2;i<=n;i++) f[1][i]=dis(p[1],p[i]);
    for (int i=2;i<=n;i++)
        for (int j=i;j<=n;j++)
            f[i][j]=min(f[i-1][j]+dis(p[i-1],p[i]),f[i-1][i]+dis(p[i-1],p[j]));
            //第一种是给走得慢的人直接分配下一个点（因为所有点都需要被分配，他不能跳着走），第二种是让走得快的人跳着走一步。
    cout<<f[n][n]<<endl;
    return 0;
}

贪心

Easy

合并果子

可以发现，这样的问题和数据结构课程中的哈夫曼树构建过程几乎一模一样。利用STL的priority_queue（内部是用堆实现的）或者自己写个堆即可轻松解决，时间复杂度$O(n\lg n)$。上机考试/比赛遇到类似的题目时可以瞎猜结论交上去，比如这道题的结论就很符合我们的直觉：不断地把最小的两堆合并。但是作为平时、作为这门算法分析课程的题目而言，我们需要研究证明这样的算法为什么正确。参见《算法导论》以及网络上各种哈夫曼树最优性证明，此处不多赘述。

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include <iostream>
#include <queue>
using namespace std;
const int maxn=11111;
int n;
priority_queue<int,vector<int>,greater<int>> h;//heap 
int main()
{
    cin>>n;
    for (int i=1;i<=n;i++) 
    {
        int x;
        cin>>x;
        h.push(x);
    }
    int ans=0;
    while (h.size()>1)
    {
        int a=h.top();
        h.pop();
        int b=h.top();
        h.pop();
        ans+=a+b;
        h.push(a+b);
    }
    cout<<ans<<endl;
    return 0;
}

铺设道路

算法设计与证明

做题时的思路：

发现如果右边一段比左边深的话，就一定产生花费；如果比左边一段浅或者相同，就可以趁左边的填充的同时一起填，不产生花费。凭感觉这样就是最优的。构造几组数据发现都是对的，那它多半就是对的，先交了试试。

一种证明思路：

设深度数组为$a$，其中增加一项$a[0]=0$和一项$a[n+1]=0$，定义差分数组$d[i]=a[i]-a[i-1]$。则将道路填平即等价于将$d[1\sim n+1]$都变成$0$。由于每一次填充操作最多将$d$的一位$+1$，另一位$-1$，因此填充次数$m\ge \sum_{d[i]>0} d[i]$才可能达成目标。下面证明必定存在填充次数$m=\sum_{d[i]>0} d[i]$的可行方法。

首先，由于$a[0]=a[n+1]=0$，因此$\sum_{i=1}^{n+1}d[i]=0$，而每一次填充操作都可以将一个正数$d[l]-1$，同时将一个负数$d[r]+1$，其中$l<r$。但填充操作并不是可以任意选择的，是有限制条件的：$l$和$r$之间（包括$l$，不包括$r$）的每个位置此时的深度都不为$0$。现在我们提供一种方法：每一次操作都将大于0的第一个，记为$d[l]$的值-1；将第一个小于0的记为$d[r]$的值+1。如果能证明这样的方法必定可行，那就证明了存在$m=\sum_{d[i]>0} d[i]$的方法。

假设这样选择的$l$和$r$之间存在深度为$0$的位置$k$，则$\sum_{i=1}^k d[i]=a[k]=0$。而$l\le k<r,d[l]>0$，因此
$$
(\sum_{i=1}^{k}d[i])-d[l]=-d[l]\
\sum_{i=1}^{l-1}d[i]+\sum_{i=l+1}^{k}d[i]<0\
$$
故$d[1\sim k]$中必有至少一项小于$0$，与“$d[r]$是最左边的一个小于$0$的”矛盾。

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
#include <iostream>
using namespace std;
const int maxn=111111;
int n,a[maxn];
int main()
{
    cin>>n;
    for (int i=1;i<=n;i++) cin>>a[i];
    int ans=0;
    for (int i=1;i<=n;i++) if (a[i]>a[i-1]) ans+=a[i]-a[i-1];
    cout<<ans<<endl;
    return 0;
}

Medium

卡牌游戏

思路

田忌赛马。对于Rachel的每一张牌，都尝试用刚好小一点的牌去对抗，因为太小的就比较“浪费”。这样的思路很符合我们的直觉。代码利用STL的map可以很方便实现。

对这种方法的证明：

由于每张牌的出牌顺序与答案无关，对Rachel的牌排序之后就可以邻项交换法（证明这种分配方式在交换相邻两个选择后只会使结果不变或更劣）很方便证明。但是不排序、直接做也是可以保证正确性的，因为这时候牌与牌之间没有顺序，可以把上面的邻项交换法稍微改动一下——任意两项交换后，能证明结果都是不变或者更劣的。

Hard部分的“国王游戏”一题将利用邻项交换法证明，作为这种方法的一个例子。

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <cstdio>
#include <algorithm>
#include <map>
using namespace std;
const int maxn=111111;
int a[maxn],n,m,ans;
map<int,int> w;
int main()
{
    scanf("%d",&n);
    for (int i=1;i<=n;i++) scanf("%d",a+i);
    scanf("%d",&m);
    for (int i=1;i<=m;i++)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        w[y]+=x;
    }
    for (int i=1;i<=n;i++)
    {
        auto it=w.lower_bound(a[i]);//it是大于等于a[i]的第一个位置，我们要找的是小于a[i]的最后一个位置
        if (it!=w.begin())//如果相等就说明没有比a[i]更小的元素
        {
            --it;
            ++ans;
            it->second--;
            if (it->second==0) w.erase(it);
        }
    }
    printf("%d\n",ans);
    return 0;
}

离线缓存

思路

刚开始的$k$个直接放进缓存。之后每遇到一个不在缓存中的数x，都与缓存中下一次出现位置最远的数y相比较，如果x将会更快出现，则替换之，否则不替换。实现时应先预处理出每个位置的数的下一次出现位置。利用priority_queue就可以解决问题。

证明：

https://www.cs.princeton.edu/courses/archive/spr05/cos423/lectures/04greed.pdf

https://blog.henrypoon.com/blog/2014/02/02/proof-of-the-farthest-in-future-optimal-caching-algorithm/

（笔者怕自己水平不够，写出来的东西容易让人看不懂，故找了看起来较合适的证明贴于此处）

蛤

思路

首先想到一个朴素贪心：模拟每只蛤的跳跃过程，一只接一只模拟，跳的时候每次都尽量跳得更远。

证明：

假设有$l$，$r$两块石头，其中$l$在$r$左边，$L$，$R$两只蛤，$L$在$R$左边，且$l$，$r$均在$R$右边。第一种情况：$L$能够跳到$l$和$r$，那么$R$一定也能跳到这两块石头，那么不管$L$跳到哪块，$R$跳到另一块，结果都是一样的（因为两只蛤是等价的，跳完的结果都是$l$和$r$的位置上各有一只蛤），不会更劣。第二种情况：$L$能够跳到$l$但跳不到$r$，那么如果$R$选择跳到$l$，就会导致$L$无处可跳，因此$R$跳到更远的$r$是更优的。第三种情况：$L$无法跳到$l$和$r$的任何一个，那么$R$无论跳到哪里，也改变不了$L$无法继续前进的情况，因此$R$的决策也不会使结果更劣。综上，$R$选择尽量远的能跳到的石头不会更劣，只可能更优。因此每次都跳得尽量远是使得最多蛤能过河的方法。

但是这样直接模拟的时间复杂度将会是$O(mn)$的，无法通过。

我们可以换一种思考方式。既然让蛤跳到离它最远的石头是最优的，其实也很容易证明，将每块石头依次分配给离它最远的蛤是最优的（按照上面证明步骤中的假设，即$l$应当选择让$L$跳过来会是可能更优、不会更劣的）（也很容易证明：每块石头都被用到比一部分石头不被用到 不会更劣）。刚才的方法是蛤选择跳哪个石头，现在的方法是石头选择让哪只蛤跳过来。也就是说，

image-20220127222024873

image-20220127222114181

image-20220127222146697

图中所示这样的方法也是一种最优的方案。

可以利用队列存储蛤们的位置，按顺序枚举石头，保持队列中的蛤的位置是递增的（每一只蛤改变位置之后都插到最后去)。如果队首的蛤跳不到最近的没跳过的石头，那它就到不了对岸。

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include <cstdio>
#include <queue>
using namespace std;
const int maxn=1111111;
int n,m,D,L,a[maxn],T;
int main()
{
    scanf("%d",&T);
    while (T--)
    {
        scanf("%d%d%d%d",&n,&m,&D,&L);
        for (int i=1;i<=n;i++) scanf("%d",a+i);
    	a[n+1]=L;
    	queue<int> q;
    	for (int i=1;i<=m;i++) q.push(0);
    	for (int i=1;i<=n+1;i++)
   		{
        	while (!q.empty()&&q.front()+D<a[i]) q.pop();
        	q.push(a[i]);
            q.pop();
    	}
    	if (q.size()==m) puts("Excited");
    	else printf("%d\n",q.size());
    }
    return 0;
}

Hard

国王游戏

思路

设众人左手上的数为$a[i]$，右手为$b[i]$，得到的奖赏为$v[i]$。则利用邻项交换法推导，
$$
v[i]=\frac{\prod_{j=0}^{i-1}a[j]}{b[i]}\
若将其中的第p项与第p+1项交换\
设s=\prod_{j=0}^{p-1}a[j]\
v[p]=\frac s {b[p]},v[p+1]=\frac{s\cdot a[p]}{b[p+1]}\
交换后v’[p]=\frac s {b[p+1]},v’[p+1]=\frac{s\cdot a[p+1]}{b[p]}\
式1:若\max{\frac 1 {b[p]},\frac{a[p]}{b[p+1]}}>\max{\frac{1}{b[p+1]},\frac{a[p+1]}{b[p]}}，则一定是交换后更优(奖赏的最大值可能更小)\
由于a[p+1]\ge 1,a[p]\ge 1,故\frac{a[p+1]}{b[p]}\ge\frac 1 {b[p]},\frac{a[p]}{b[p+1]}\ge\frac{1}{b[p+1]}\
故只有当\frac{a[p+1]}{b[p]}<\frac{a[p]}{b[p+1]}时，式1才会成立,交换后才会更优\
即a[p]\cdot b[p]>a[p+1]\cdot b[p+1]时应当交换\
故应当按照a[x]\cdot b[x]的值排序，贪心选取
$$
但本题需要高精度才能拿到满分，但那不是本题的重点。

参考代码

没写高精度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include <iostream>
#include <algorithm>
using namespace std;
const int maxn=1111;
int n;
pair<int,int> d[maxn];
bool cmp(const pair<int,int> &x,const pair<int,int> &y)
{
    return (long long)x.first*x.second<(long long)y.first*y.second;
}
int main()
{
    cin>>n;
    for (int i=0;i<=n;i++) cin>>d[i].first>>d[i].second;
    sort(d+1,d+n+1,cmp);
    long long now=d[0].first,ans=0;
    for (int i=1;i<=n;i++) 
    {
        ans=max(ans,now/d[i].second);
        now*=d[i].first;
    }
    cout<<ans<<endl;
    return 0;
}

最大流

写在前面

这一段主要讲述建模方法，由于求解方法在《算法导论》中已有比较详细的阐述。下文默认读者已经了解二分图匹配和最大流问题的基本定义和实现方法。

给出的建模方法都只是示例，可能有其它结果相同的建模方法，比如很多情况下将所有边反向后的答案不变。

最大流问题的建模方法大致可以分为利用最大流的思路建模以及利用最小割的思路建模。其中最小割思路常常应用于“在一些物品中选择一些已得到最优结果”时，不选择物品在建模中的体现便是被割掉，选择该物品则是对应的边不被割掉。

笔者所用的最大流ISAP算法（dinic的改进算法）模板（使用数组模拟的链式前向星存图法，一般只会在竞赛中使用而几乎没有实际使用价值，请读者不要盲目模仿）以及其它宏定义如下。为避免篇幅过长，每道题的参考代码中将不再复制。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
//by Richard
#include <bits/stdc++.h>
#include <bits/extc++.h>
#define mp make_pair
#define cls(x) memset(x,0,sizeof(x))
#define rep(x,y,z) for (int x=(y);(x)<=(z);(x)++)
#define per(x,y,z) for (int x=(y);(x)>=(z);(x)--)
const int inf=0x3f3f3f3f;
using namespace std;
typedef long long LL;
typedef pair<int,int> pairs;
///////////////////////read5.1///////////////////////
template<typename T>
inline void read(T &x){char ch;x=0;bool flag=false;ch=getchar();while (ch>'9'||ch<'0') {if (ch=='-') flag=true;ch=getchar();}while ((ch<='9'&&ch>='0')){x=x*10+ch-'0';ch=getchar();}if (flag) x*=-1;}
template<typename T,typename U>
inline void read(T &x,U &y){read(x);read(y);}
template<typename T,typename U,typename V>
inline void read(T &x,U &y,V &z){read(x);read(y);read(z);}
////////////////variables&functions//////////////////
struct EDGE
{
    int u,v,w;
};
const int MAXV=10000,MAXE=40000;
struct GRAPH
{
    EDGE edge[MAXE];
    int next[MAXE],first[MAXV],cnt,v=0;
    void init(int vv)
	{
        memset(first,-1,sizeof(first));
        cls(edge);cls(next);
        cnt=-1;v=vv;
    }
    void addedge(int u,int v,int w)
	{
        edge[++cnt].u=u;edge[cnt].v=v;
        edge[cnt].w=w;next[cnt]=first[u];
        first[u]=cnt;edge[++cnt].u=v;
        edge[cnt].v=u;edge[cnt].w=0;
        next[cnt]=first[v];first[v]=cnt;
    }
}graph;
int SAP(int S,int T)
{
    static int current[MAXE],distance[MAXV],layer[MAXV],last[MAXV],pred[MAXV];
    rep(i,0,graph.v)
    {
        current[i]=graph.first[i];
        distance[i]=layer[i]=0;
    }
    int i=S,now_flow=inf,total_flow=0;
    while (distance[S]<graph.v)
    {
    xxx:
        last[i]=now_flow;
        for (int k=current[i];k!=-1;k=graph.next[k])
        {
            int j=graph.edge[k].v;
            if ((!graph.edge[k].w)||distance[i]!=distance[j]+1) continue;
            current[i]=k;
            int cur_flow=graph.edge[k].w;
            now_flow=min(cur_flow,now_flow);
            pred[j]=i;
            i=j;
            if (i==T)
            {
                total_flow+=now_flow;
                while (i!=S)
                {
                    i=pred[i];
                    graph.edge[current[i]].w-=now_flow;
                    graph.edge[current[i]^1].w+=now_flow;
                }
                now_flow=inf;
            }
            goto xxx;
        }
        int min_dis=graph.v-1,min_place=-1;
        for (int k=graph.first[i];k!=-1;k=graph.next[k])
        {
            int j=graph.edge[k].v;
            if (graph.edge[k].w&&distance[j]<min_dis)
            {
                min_dis=distance[j];
                min_place=k;
            }
        }
        current[i]=min_place;
        layer[distance[i]]--;
        if (!layer[distance[i]]) break;//gap
        distance[i]=min_dis+1;
        layer[distance[i]]++;
        if (i!=S) {i=pred[i];now_flow=last[i];}
    }
    return total_flow;
}

Naive

搭配飞行员

本题完全符合二分图匹配的定义。直接利用匈牙利算法求解即可。

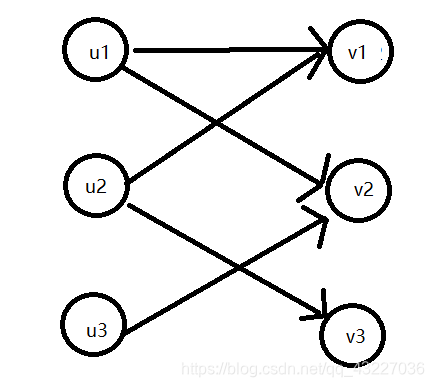
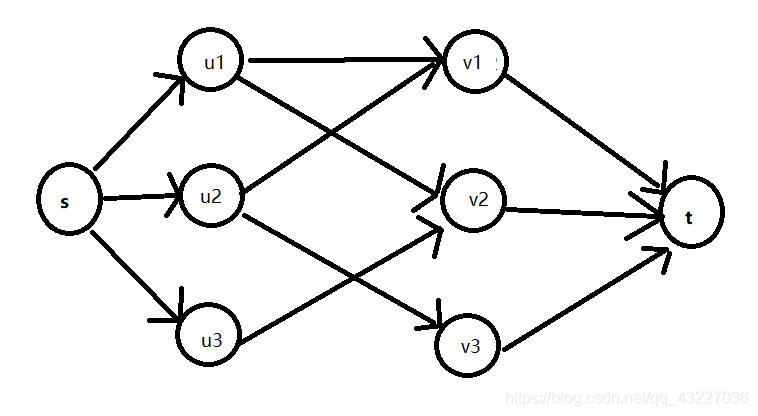
当然，二分图匹配问题均可转化为最大流问题。建立一个超级源点S(source)和一个超级汇点T(terminal)，从S向每一个正驾驶员都连一条流量为1的边，从每一个副驾驶员向T连一条流量为1的边，并从配对的正驾驶员向副驾驶员连边。最大流的答案即二分图匹配的答案。

下面是网上找的图片 第一张是二分图匹配的建模方式，第二张是最大流的建模方式

在这里插入图片描述

在这里插入图片描述

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
int n,m;
bool did1[MAXV],did2[MAXV];
int main()
{
    read(n,m);
    graph.init(n+2);
    int u,v;
    while (cin>>u>>v) 
    {
        if (!did1[u])
        {
            did1[u]=true;
            graph.addedge(n+2,u,1);
        }
        if (!did2[v])
        {
            did2[v]=true;
            graph.addedge(v,n+1,1);
        }
        graph.addedge(u,v,1);
    }
    cout<<SAP(n+2,n+1)<<endl;
    return 0;
}

Easy

试题库

最大流基础建模方法。将每道题都看成点，将每个类别也看成点，再设一个超级源点S和一个超级汇点T。从S向每道题连一条容量为1的边，从每道题向所属的各个类别分别连容量为1的边，从各个类别向T连容量为所需题数的边。判断最大流是否等于m即可。

本题的另一个要求是输出方案。判断最大流算法结束后S向每道题连的边的流量，若1则选中该题，若0则未选中。

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
int n,k,a[MAXV],m,p[MAXV];
vector<int> v[MAXV],ans[MAXV];
int S,T;
void dfs(int x,int step)
{
    for (int q=graph.first[x];q!=-1;q=graph.next[q])
    {
        int j=graph.edge[q].v;
        if (j==S) continue;
        if (step==0) dfs(j,step+1);
        else
        {
            if (graph.edge[q].w==0) ans[x].push_back(j-k);
        }
    }
}
int main()
{
    read(k,n);
    rep(i,1,k) {read(a[i]);m+=a[i];}
    rep(i,1,n) 
    {
        read(p[i]);
        int x;
        rep(j,1,p[i]) 
        {
            read(x);
            v[i].push_back(x);
        }
    }
    S=n+k+1,T=n+k+2;
    graph.init(n+k+2);
    rep(i,1,k) graph.addedge(S,i,a[i]);
    rep(i,1,n)
        for (auto to:v[i]) graph.addedge(to,i+k,1);
    rep(i,1,n) graph.addedge(i+k,T,1);
    int flow=SAP(S,T);
    if (flow!=m)
    {
        cout<<"No Solution!"<<endl;
        return 0;
    }
    dfs(S,0);
    rep(i,1,k)
    {
        cout<<i<<":";
        for (auto to:ans[i]) cout<<' '<<to;
        cout<<endl;
    }
    return 0;
}

圆桌聚餐

二分图多重匹配。与上面的题目非常相似的建模方法。

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
int n,m,S,T;
int main()
{
    read(n,m);
    graph.init(n+2+m);
    S=n+m+1;T=n+m+2;
    int sum=0;
    rep(i,1,n) 
    {
        int x;
        read(x);
        graph.addedge(S,i,x);
        sum+=x;
    }
    rep(i,1,m)
    {
        int x;
        read(x);
        graph.addedge(i+n,T,x);
    }
    rep(i,1,n) rep(j,1,m) graph.addedge(i,j+n,1);
    int ans=SAP(S,T);
    if (ans==sum) cout<<1<<endl;
    else {cout<<0<<endl;return 0;}
    rep(i,1,n)
    {
        vector<int> v;
        for (int k=graph.first[i];k!=-1;k=graph.next[k])
        {
            int j=graph.edge[k].v;
            if (j==S) continue;
            if (!graph.edge[k].w) v.push_back(j-n);
        }
        sort(v.begin(),v.end());
        for (auto to:v) cout<<to<<' ';
        cout<<endl;
    }
    // cout<<ans<<endl;
    return 0;
}

迷宫

思路

首先看到这道题并不像传统的最大流题目，询问的不是最多能通过几个人，而是最短几天可以让人们都通过。乍一看似乎很难用网络流相关算法解决。然而贪心、最短路等图论常用解题思路也都无能为力。

考虑把题目转化成“最多能通过几个人”的问题：二分答案。（二分答案：二分最终所求的答案的值，每一轮都检查当前的mid值是否可行，从而得到最大/小的可行/不可行答案，具体可以请教网络）

本题在二分答案的基础上就只需要考虑这样的问题：检查当前所确定的mid天内最多能通过的人数是否大于等于总人数。

如果没有接触过这样的题目，可能难以马上想到建模的方法。

其实可以将同一个点在不同日子看成不同的点（也可以说是把原本的一个点拆成了“时间”个点），将i号点在第n天时记作i,n，如1号点在第1天时记作1,1、2号点在第3天时记作2,3

如果i号点到j号点存在一条容量为w的有向边，就从i,1向j,2连边，从i,2向j,3连边，从i,n向j,n+1连边，这些边的容量都是w

同时，对于每一个点，由于每个点都可以供任意多人停留，所以对于每个点都从i,n向i,n+1连容量为无穷的边

以这样的方法设置点和边，从而建立一个分层图，最大流即为最多能通过的人数。

image-20220203202803406

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
int m,V,E,S,T;
int x[MAXE],y[MAXE],c[MAXE];
bool check(int d)//number of days
{
    graph.init((d+1)*V);
    rep(i,1,d) 
    {
        rep(j,1,V) graph.addedge(j+(i-1)*V,j+i*V,inf);
        rep(j,1,E) graph.addedge(x[j]+(i-1)*V,y[j]+i*V,c[j]);
    }
    return SAP(S,T+d*V)>=m;
}
int main()
{
    read(m,V,E);read(S,T);
    rep(i,1,E) read(x[i],y[i],c[i]);
    if (S==T) {cout<<0<<endl;return 0;}
    int l=1,r=200;
    while (l<r)
    {
        int mid=(l+r)>>1;
        if (check(mid)) r=mid;
        else l=mid+1;
    }
    cout<<l<<endl;
    return 0;
}

Medium

逃逸问题

思路

路径互不相交等价于每个节点最多被经过一次。容易发现，只加入“每条边最多被经过一次”的限制会导致两条路径可能经过同一个节点，与本题题意不符。但最大流建模只能限制边的流量而不能限制点的流量，应该怎么办呢？

一个知道了就觉得很显然的方法：把每个节点拆成两个点，在两个拆出来的点之间连一条容量为1的边。

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
int n,m;
inline int id(int x,int y,int z){return y+(x-1)*n+z*n*n;}
int main()
{
    read(n,m);
    int S=0,T=2*n*n+1;
    graph.init(2*n*n+1);
    rep(i,1,m) 
    {
        int x,y;
        read(x,y);
        graph.addedge(0,id(x,y,0),1);
    }
    rep(i,1,n) rep(j,1,n)
    {
        graph.addedge(id(i,j,0),id(i,j,1),1);
        if (i>0) graph.addedge(id(i,j,1),id(i-1,j,0),1);
        if (i<n) graph.addedge(id(i,j,1),id(i+1,j,0),1);
        if (j>0) graph.addedge(id(i,j,1),id(i,j-1,0),1);
        if (j<n) graph.addedge(id(i,j,1),id(i,j+1,0),1);
        if (i==1||j==1||i==n||j==n) graph.addedge(id(i,j,1),T,1);
    }
    if (SAP(S,T)==m) cout<<"YES"<<endl;
    else cout<<"NO"<<endl;
    return 0;
}

方格取数

思路

容易发现，方格可以类似国际象棋棋盘进行划分，一半黑一半白，同颜色格子之间互不相邻。任意两个数之间没有公共边，即任意相邻格子都不能同时被选择。

那么我们就可以把黑格和白格分别看成二分图（二部图）的一部。题目所求问题即为“二分图最大点权独立集”（独立集意为选择一些点，使它们互相没有相连的边）。

题目所要求的答案是最大能同时选择的数字和，也就等于所有数字总和减去无法选的数字的和，由最大流最小割定理，如果“最小的无法选的数字和”可以转化为一个最小割模型，那么它就能用最大流算法解决。

设置一个超级源点S和一个超级汇点T，从S向所有黑色格子连容量为该格数字的边，从所有白色格子向T连容量为该格数字的边。从所有黑色格子向相邻的白色格子连容量为无穷大的边（由于容量无穷大，这样的边不会在最小割问题中被割掉）。这样建图后，求解最小割时，只可能割去S到黑色格子的边（表示该格不被选择）以及白色格子到T的边（也表示该格不被选择）。若某处存在从S到T的未用完的流量，则说明互相排斥的两个格子同时被选择，因此去掉最小割后选择的格子必定不互相排斥，且最小割割掉的数字和最小，因此是最优解。

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
const int maxn=33;
int n,m,a[maxn][maxn],S,T;
inline int c(const int &x,const int &y){return (x-1)*n+y;}
int main()
{
    read(m,n);
    int sum=0;
    rep(i,1,m) rep(j,1,n) {read(a[i][j]);sum+=a[i][j];}
    graph.init(10000);
    S=m*n+1;T=m*n+2;
    rep(i,1,m) rep(j,1,n) if ((i+j)&1) graph.addedge(S,c(i,j),a[i][j]);
    rep(i,1,m) rep(j,1,n) if (!((i+j)&1)) graph.addedge(c(i,j),T,a[i][j]);
    rep(i,2,m) rep(j,1,n) if ((i+j)&1) graph.addedge(c(i,j),c(i-1,j),inf);
    rep(i,1,m) rep(j,2,n) if ((i+j)&1) graph.addedge(c(i,j),c(i,j-1),inf);
    rep(i,1,m-1) rep(j,1,n) if ((i+j)&1) graph.addedge(c(i,j),c(i+1,j),inf);
    rep(i,1,m) rep(j,1,n-1) if ((i+j)&1) graph.addedge(c(i,j),c(i,j+1),inf);
    int ans=sum-SAP(S,T);
    // cout<<sum<<endl;
    cout<<ans<<endl;
    return 0;
}

Hard

太空飞行计划

思路

发现这道题仍是“物品选择”问题，考虑最小割的思路。设置一个超级源点S，一个超级汇点T，从S向每个实验连接容量为$p_j$的边，从相联系的实验向仪器各连容量为无穷大的边，从仪器向T连容量为$c_k$的边。最终答案即为$\sum p-最小割$。

S到实验的边若被割掉，代表实验未被选择（因为不选择某个实验会亏钱，相当于会花钱）。仪器到T的边若被割掉，代表仪器被选择（因为选择仪器需要花钱）。若某处存在S到T的未用完的流量，则说明实验被选择且对应的仪器并没有被全部选择，显然并不是符合题意的情况。而最小割的情况下就可以保证所有被选择的实验对应的仪器均被选择。

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
bool vis[MAXV];
void dfs(int x)
{
    vis[x]=1;
    for (int k=graph.first[x];k!=-1;k=graph.next[k])
    {
        int j=graph.edge[k].v;
        if (!vis[j]&&graph.edge[k].w) dfs(j);
    }
}
int n,m;
int main()
{
    read(m,n);
    graph.init(n+2+m);
    LL ans=0;
    rep(i,1,m)
    {
        int w;
        read(w);
        ans+=w;
        graph.addedge(n+m+1,i,w);
        string s;
        getline(cin,s);
        stringstream ss(s);
        int x;
        while (ss)
        {
            ss>>x;
            graph.addedge(i,x+m,inf);
        }
    }
    int x;
    rep(i,1,n)
    {
        read(x);
        graph.addedge(i+m,n+m+2,x);
    }
    dfs(n+m+1);
    rep(i,1,m) if (vis[i]) cout<<(i!=1?" ":"")<<i;
    cout<<endl;
    rep(i,1,n) if (vis[i+m]) cout<<(i!=1?" ":"")<<i;
    cout<<endl;
    cout<<ans-SAP(n+m+1,n+m+2)<<endl;
    return 0;
}

拓展

本题实际上是最大权闭合子图模型的一个特殊情况（二分图）

最大权闭合子图
定义

一张有向图中，每个点都有一个权值。定义闭合子图为一个点集和点集内所有点之间的边组成的图，满足若某个点在点集内，则它的后继点也在点集内。当点集的权值和最大时，称作最大权闭合子图。

求法

该问题事实上可以转化为最小割问题。从S对每一个正权点连一条流量为权值的边，从每个负权点对T连一条流量为权值绝对值的边，将点之间的边的流量设为正无穷，则原图除去最小割即为最大权闭合子图。

证明

  1. 割边的含义

    由于原图的边都是无穷大，那么割边一定是与S或T相连的。

    割掉S与x的边，表示不选择x点作为子图的点
    割掉x与T的边，表示选择x点为子图的点

    如果S与x有边，表示x存在子图中
    如果x与T有边，表示x不存在于子图中

  2. 只有S与T不连通，图才是闭合子图

    若S与T联通，则必然存在一组点x,y,使得S->x->y->T。则据1的定义，x存在于子图中，y不存在于子图中，则与闭合子图定义矛盾

  3. 只要S与T不连通，图即为闭合子图（求最小割的过程中）

    首先剩余的图必定为原图的子图。若某个正权点被选择了，则它指向的所有负权点必然没有被选择。对于正权点指向的别的正权点，最小割过程中将不会割去它(割去的操作只会减小流量而不会断流因此没有收益)

  4. 最小割为最优方案

    最小割=(不选的正权和+要选的负权绝对值和）
    最大权闭合子图=（正权和-不选的正权和-要选的负权绝对值和）=正权和-最小割
    因为正权和是定值，而最小割保证值最小，所以最大权闭合子图一定最优。

参考:https://my.oschina.net/u/4417528/blog/3943851

最小路径覆盖

思路

将题给的每个点拆成两个点，形成一张二分图。设$x$点拆成$x_1$与$x_2$两个点。则若原图中存在$x$到$y$的有向边，则添加一条$x1$指向$y2$的边。原图的点数减去新图的二分图最大匹配（做法参考搭配飞行员）即为答案。

首先，若不存在任何边，显然答案为原图点数。否则，把拆成的两个点$x_1$当作出点，$x_2$当作入点。每当新图中有一个匹配，即意味着匹配中的某个$x_1$可以连到$y_2$，则原本的$pre\rightarrow x$以及$y\rightarrow nxt$($pre$和$nxt$表示已存在的在$x$结束/从$y$开始的路径，且可以为空)两条路径显然可以变为$pre\rightarrow x\rightarrow y\rightarrow nxt$一条路径，减少了一条，答案减一。要求最小路径覆盖，即要求此处的匹配数最大，因此可以利用二分图匹配解决。

参考代码

1
int n,m,nxt[MAXV];bool visited[MAXV];vector<pairs> v;void dfs(int x,int last){	visited[x]=true;	for (int k=graph.first[x];k!=-1;k=graph.next[k])	{		int j=graph.edge[k].v;		if (visited[j]) continue;		if (j==2*n+2) 		{			v.push_back(mp(last,x-n));			return;		}		dfs(j,x);	}}bool done[MAXV];int main(){	read(n,m);	graph.init(2*n+2);	rep(i,1,n) graph.addedge(2*n+1,i,1);	rep(i,1,n) graph.addedge(i+n,2*n+2,1);	rep(i,1,m)	{		int u,v;		read(u,v);		graph.addedge(u,v+n,1);	}	int ans=n-SAP(2*n+1,2*n+2);	dfs(2*n+1,-1);	for (auto to:v)	nxt[to.first]=to.second;	rep(i,1,n) 	{		if (!done[i]) 		{			for (int j=i;j;j=nxt[j])			{				done[j]=true;				cout<<j<<' ';			}			cout<<endl;		}	}	cout<<ans<<endl;	return 0;}

最短路

Easy

小K的农场

差分约束的模板题，做法请看《算法导论》。下面的代码用了bellman-ford算法，有兴趣的同学可以自行研究一种该算法的优化——SPFA。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#include <iostream>
#include <vector>
#include <cstring>
using namespace std;
const int maxn=11111;
int n,m,dis[maxn];
struct Edge
{
    int u,v,w;
};
vector<Edge> e;
void addedge(int u,int v,int w)
{
    e.push_back({u,v,w});
}
bool check()
{
    memset(dis,0x3f,sizeof(dis));
    dis[0]=0;
    for (int i=1;i<=n;i++)
    {
        for (auto t:e)
            if (dis[t.v]>dis[t.u]+t.w) dis[t.v]=dis[t.u]+t.w;
    }
    for (auto t:e)
        if (dis[t.v]>dis[t.u]+t.w) return false; 
    return true;
}
int main()
{
    cin>>n>>m;
    for (int i=1;i<=n;i++) addedge(0,i,0);
    for (int i=1;i<=m;i++) 
    {
        int op,a,b,c;
        cin>>op;
        if (op==1) 
        {
            cin>>a>>b>>c;
            addedge(a,b,-c);
        }
        else if (op==2)
        {
            cin>>a>>b>>c;
            addedge(b,a,c);
        }
        else 
        {
            cin>>a>>b;
            addedge(a,b,0);
            addedge(b,a,0);
        }
    }
    if (check()) cout<<"Yes"<<endl;
    else cout<<"No"<<endl;
    return 0;
}

Medium

Bitonic Shortest Paths

即《算法导论》思考题24-6，双调最短路径

思路

题目中所说的合法的双调序列并非一定是先单调增长再单调递减（因为还可以循环移位）。更通用的说法应该是最多有两段先单调增长再单调递减的序列（可能是上、下、上下、下上、上下上、下上下、上下上下、下上下上），也就是最多两段下两段上。

We’ll use the Bellman-Ford algorithm, but with a careful choice of the order in which we relax the edges in order to perform a smaller number of $\text{RELAX}$ operations. In any bitonic path there can be at most two distinct increasing sequences of edge weights, and similarly at most two distinct decreasing sequences of edge weights. Thus, by the path-relaxation property, if we relax the edges in order of increasing weight then decreasing weight twice (for a total of four times relaxing every edge) the we are guaranteed that $v.d$ will equal $\delta(s, v)$ for all $v \in V$ . Sorting the edges takes $O(E\lg E)$. We relax every edge $4$ times, taking $O(E)$. Thus the total runtime is $O(E\lg E) + O(E) = O(E\lg E)$, which is asymptotically faster than the usual $O(VE)$ runtime of Bellman-Ford.

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
const int maxn=1000001,maxm=1000001;
int s,n,m;
struct Edge
{
    int u,v;
    double w;
    bool operator<(const Edge &b)const
    {
        return w>b.w;
    }
}e[maxm];
double dis[maxn];
int main()
{
    scanf("%d%d%d",&n,&m,&s);
    for (int i=1;i<=m;i++) scanf("%d%d%lf",&e[i].u,&e[i].v,&e[i].w);
    sort(e+1,e+m+1);
    for (int i=1;i<=n;i++) dis[i]=1e18;
    dis[s]=0;
    for (int i=1;i<=m;i++) dis[e[i].v]=min(dis[e[i].v],dis[e[i].u]+e[i].w);
    for (int i=m;i>=1;i--) dis[e[i].v]=min(dis[e[i].v],dis[e[i].u]+e[i].w);
    for (int i=1;i<=m;i++) dis[e[i].v]=min(dis[e[i].v],dis[e[i].u]+e[i].w);
    for (int i=m;i>=1;i--) dis[e[i].v]=min(dis[e[i].v],dis[e[i].u]+e[i].w);
    for (int i=1;i<=n;i++) printf("%.6lf\n",dis[i]);
    return 0;
}

Hard

最短路

思路

本题如果直接从单源最短路的经典模型思考，会发现求解过程中很难体现电量不够到不了的这个限制。怎么办？

把可以充电的点看作重要点。由于终点是否是充电点不影响答案，我们可以认为终点是重要点，同时起点一定是重要点，所以如果能将原图重构成一张使答案不变的、包含可达信息的、只包含重要点的图之后，就能用一次单源最短路算法dijkstra求得答案。

我们考虑从某个重要点a出发后不充电能达到的所有重要点，并求出从a出发到各点的最短路。这个问题非常容易解决，以a为源点跑一遍dijkstra，如果有与a距离小于等于k的重要点b，就在重构图中加一条边（从a到b，距离为此处的最短路）。对每个重要点都进行一次这样的操作，复杂度可以优化到$O(n^2\lg n)$。

加上最后一遍对于重构后的图的dijkstra，总复杂度仍然是$O(n^2\lg n)$。

以样例数据为例，标黄的点为重要点

image-20220207125352138

重构后的图：

image-20220207130105596

参考代码

该代码没有经过各种优化，是最暴力的堆优化dijkstra。但已经完全可以通过本题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
#include <iostream>
#include <algorithm>
#include <cstring>
#include <queue>
using namespace std;
const int maxn=1111;
int n,m;
bool b[maxn],did[maxn];
long long dis[maxn],k;
vector<pair<int,long long>> e[maxn],ee[maxn];
struct cmp
{
    bool operator()(const pair<int,long long> &a,const pair<int,long long> &b)
	{
        return a.second>b.second;
    }
};
int main()
{
    cin>>n>>m>>k;
    for (int i=1;i<=n;i++) cin>>b[i];
    b[n]=1;
    for (int i=1;i<=m;i++) 
    {
        int u,v,w;
        cin>>u>>v>>w;
        e[u].push_back({v,w});	
        e[v].push_back({u,w});
    }
    for (int i=1;i<=n;i++) if (b[i])
    {
        memset(dis,0x3f,sizeof(dis));
        memset(did,0,sizeof(did));
        dis[i]=0;
        priority_queue<pair<int,long long>,vector<pair<int,long long>>,cmp> q;
        q.push({i,0});
        while (!q.empty())
        {
            while (!q.empty()&&did[q.top().first]) q.pop();
            if (q.empty()) break;
            pair<int,long long> now=q.top();
            did[now.first]=true;
            q.pop();
            for (auto &x:e[now.first])
            {
                if (dis[x.first]>dis[now.first]+x.second) 
                {
                    dis[x.first]=dis[now.first]+x.second;
                    q.push({x.first,dis[x.first]});
                }
            }
        }
        for (int j=1;j<=n;j++) 
            if (b[i]&&b[j]&&i!=j&&dis[j]<=k) ee[i].push_back({j,dis[j]});//虽然是无向图但是这里不用连双向边，因为以j为源点跑dijkstra的时候会连一条与现在反向的边
    }
    memset(dis,0x3f,sizeof(dis));
    memset(did,0,sizeof(did));
    dis[1]=0;
    priority_queue<pair<int,long long>,vector<pair<int,long long>>,cmp> q;
    q.push({1,0});
    while (!q.empty())
    {
        while (!q.empty()&&did[q.top().first]) q.pop();
        if (q.empty()) break;
        pair<int,long long> now=q.top();
        did[now.first]=true;
        q.pop();
        for (auto &x:ee[now.first])
        {
            if (dis[x.first]>dis[now.first]+x.second) 
            {
                dis[x.first]=dis[now.first]+x.second;
                q.push({x.first,dis[x.first]});
            }
        }
    }
    cout<<dis[n]<<endl;
    return 0;
}